| 안대영의 카오스와 프랙탈 |
1. Fractal 이란 무엇인가?
프랙탈이란 전체를 부분부분으로 나누었을 때 부분안에 전체을 모습을 갖는 무한단계에서의 기하적인 도형이다. 우리가 보는 것은 유한단계의 그림을 보는 것이다. 자기닮음(self-similar, 자기유사성)과 축소에 대한 불변(independent of scale)을 갖는다.
아래 그림은 프랙탈이 아니다.
왜!
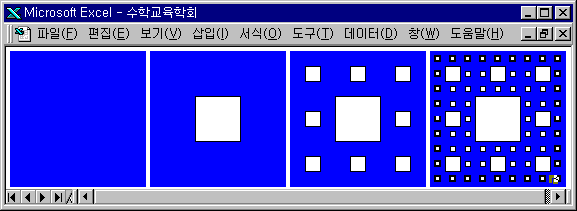
프랙탈은 무한단계의 그림이다. 실제 존재하지 않는다. 왜 무한단계이어야 하는가?
2. 축소에 대한 불변(프랙탈 차원)
자기닮음 이란 무엇인가? 자기닮음이란 도형의 각 부분들이 전체와 닮은 성질이다. 자기닮음을 지니고 있다고 해서 프랙탈은 아니다. 선, 정사각형, 정육면체, 코흐 곡선에 대해 생각해보자. 차원의 종류는 20여 가지가 있다. 다음은 일반적으로 사용하는 자기닮음 차원을 구하는 방법이다.
N : 조각의 개수, D : 프랙탈 차원 r : 축소율
N=(1/r)D 즉, D=(logN)/(log(1/r))
|
도형 |
조각의 개수 |
축소율(r) |
차원 |
|
선분 |
3 (길이 1인 선분을 3등분 했을때의 개수) |
1/3 (길이 1인 선분을 3등했을때의 길이 |
log3/log3 =1 |
|
6 |
1/6 |
log6/log6 =1 | |
|
9 |
1/9 |
log9/log9 =1 | |
|
정사각형 |
9=32(각변을 3등분) |
1/3 |
log9/log3 =2 |
|
36=62(각변을 6 등분) |
1/6 |
log36/log6 =2 | |
|
정육면체 |
27=33 |
1/3 |
log27/log3 =3 |
|
216=63 |
1/6 |
log216/log6 =3 | |
|
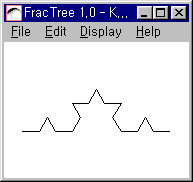
코흐곡선 |
4 |
1/3 |
log4/log3=1.26 |
|
|
16 |
1/9 |
log16/log9=1.26 |
|
|
4k |
1/(3k) |
|
●프랙탈 차원 종류 Capacity Dimension, Correlation Dimension, Fractal Dimension, Hausdorff Dimension, Information Dimension, Lyapunov Dimension, Minkowski-Bouligand Dimension, Pointwise Dimension, q-Dimension
3. 상자차원이란 무엇인가?
자기닮음 차원을 사용할 수 없는 경우가 있다. 다양한 크기의 격자를 이용하여 도형의 복잡도를 측정할 수 있다. 주어진 그림을 포함하는 상자 수를 y, 격자의 크기를 결정하는 축척 x 의 역수를 용지에 나타낸다. 표준좌표(x, y ), 준로그 좌표(x, logy), 이중로그 좌표(logx, logy)를 이용하여 자료를 분석해 보자. 상자의 개수(y)와 격자의 크기(1/x) 사이의 관계를 이중로그 그래프(log(1/x), logy)로 나타낼 때만 선형 그래프가 된다. 따라서 상자의 개수와 축척사이의 관계는 멱 관계이다. 이러한 이중로그 그래프 용지에서 얻어진 직선의 기울기는 멱함수에서의 지수이다. 이 지수는 그 도형의 프랙탈 차원을 나타내는데, 직선의 프랙탈 차원은 1, 원이나 정사각형은 2, 프랙탈 고선의 차원은 1과 2 사이이다.
●세계지도의 상자차원을 구해보자.
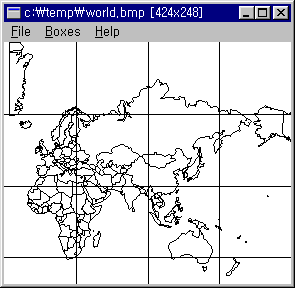
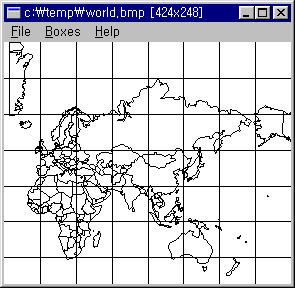
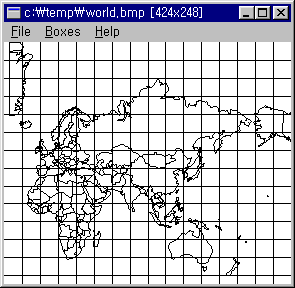
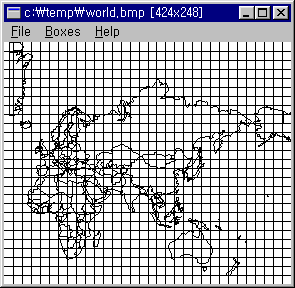
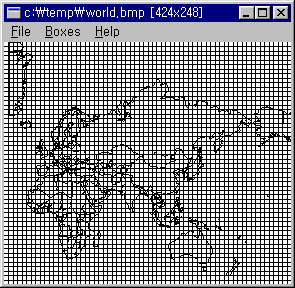
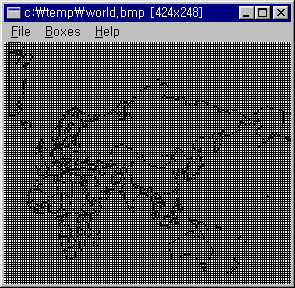
① 해안선 및 국경을 포함하는 상자를 세어보면 다음과 같다.
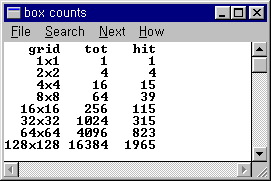
② 이중로그 그래프를 그렸다.
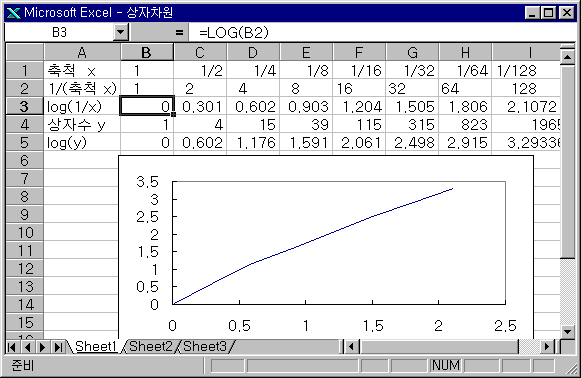
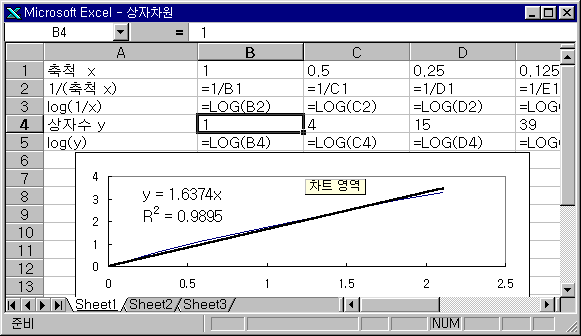
③ 직선에서 오른쪽 마우스를 클릭하여 추세선을 추가한다. 옵션메뉴에서 수식을 차트에 표현할 수 있다. 실제 입력되어 있는 내용이다. 기울기가 1.6374 이다.
즉 세계지도는 1.6347 의 프랙탈 차원을 가진다.

[예제] 칸토르 집합은 자기닮음임이다.

5. NCTM은 수학교육과정 2000 에서는 '고등학교 기하교육에 대해' 어떻게 말하고 있는가?
학생들은 좌표계, 삼각함수의 관계성, 네트웍, 일차변환, 벡터, 행렬등의 영역을 이해해야 한다. 학생들이 부딪히는 기하적인 상황은 유클리드 기하만이 아니다. 이산 그래프, 구면 기하, 프랙탈 기하등은 주어진 상황을 탐구하는데 도움을 줄 수 있다. 고등학교에서 기하교육의 목적은 물리적 세계의 이해와. 물리적 세계의 아름다움을 이해하고, 분석하고, 기술하는 수단을 제공한다.
6. 카오스란 무엇인가?
초기조건의 민감성 때문에 결정론적 계(deterministic system)에서 일어나는 예측할 수 없는 움직임이 나타난다. 초기에는 별차이 없던 것이 결국에는 예측할 수 없는 움직임이 나타난다.
7. 카오스와 프랙탈은 같은 것인가?
사람들은 혼란스러워 한다. 카오스를 이야기할 때도 카오스와 프랙탈을 함깨 언급하기 때문이다. 프랙탈과 카오스는 자연의 현상이나 대상을 모델링하는 도구이다. 카오스는 결정론적 임에도 불구하고 예측불가능성, 초기조건의 민감성을 갖는다.
많은 프랙탈은 카오스적인 성질을 갖지 않는다. (시어핀스키 삼각형, 코흐 곡선).
그렇다면 관계가 없다는 것인가?
다른 관점에서 출발하지만 공통점을 가지고 있다. 카오스적인 여러현상이 프랙탈의 성질을 갖는다는 것이다.
8. 프랙탈(fractal)이란 단어는 누가 만들었나?
1975년 만델브로트(Mandelbrot)가 '프랙탈한 대상 모양, 우연 , 차원'이라는 책을 출판하였다. 이것은 각각 수학과 과학 세계에 충격을 주었다.
프랙탈은 70년대 말부터 물리학자, 지리학자, 건축, 미술, 철학 등의 분야에서 주목을 받게 되었다. 만델브로트는 처음으로 프랙탈에 대해 많은 연구를 시작한 사람으로 자신이 생각한 형상, 차원 및 기하학에 대한 이름을 생각하고, 라틴어의 '부서지다'라는 뜻의 동사 'frangere'에서 파생한 형용사 'fractus'를 찾았다. fractus란 '온전한 것이 아닌', '어중간한', 뜻으로 어원이 같은 영어 단어 'fracture'와 'fraction'의 어감도 적절한 것으로 생각했다. 만델브로트는 영어이면서 불어이며, 명사이자 형용사인 'fractal'을 만들었다.
9. 수학에서 카오스는 누가 사용하였나?
1970년대에 요크와 이천암의 수학논문에서 처음으로 '카오스'라는 단어가 사용되었다.
10. 나비효과란 무엇인가?
아프리카 한구석에 있는 나비 한 마리의 날개짓은 바로 옆에 있는 작은 벌레를 나뭇잎에서 떨어뜨린다. 밑에서 놀고 있는 원숭이 털속에 떨어진다. 원숭이는 그 벌레 때문에 가려워 긁다가 옆의 열매를 떨어 뜨린다. 열매는 돌에 부딪쳐 돌을 구르게 한다. 돌은 큰 바위를 지탱한 작은 돌을 쳐서 밀어내면서 작은 산사태를 일으킨다. 이것은 작은 시냇물을 막고 물 흐름을 바꾸어 놓아 화산 증기 구멍을 막는다. 다시 약한 지반을 꺼지게 하면서 화산 폭발을 일으킨다. 화산재는 부분적으로 대기의 기류를 바꾸어 큰 대기압 차이를 일으키고, 급기야 지중해 상의 대류 변화를 일으켜서 북반구의 해양성 기류와 부딪히면서 유럽 대륙에 커다란 폭풍을 일으킨다.
11. 카오스는 어떻게 시작되었나?
1887년 스웨덴의 국왕 오스카 2세는 "태양계는 과연 안정된 상태인가?"라는 천문학의 오랜 궁금증을 해결하는 사람에게 상금을 준다고 발표했다. 태양과 9개의 행성, 그리고 소행성과 수많은 위성들이 안정된 궤도를 계속 돌 것인가, 아니면 어느 행성이 궤도를 이탈해 태양과 정면 충돌할 것인가의 문제이다. 뉴턴 역학은 지구의 공전주기는 태양과 지구만을 고려한 결과이다. 포앙카레(Henri Poincare)는 두 물체만을 고려해서는 안 된다고 생각했다. 그러나 지구와 달의 관계에서 태양을 고려할 때 (삼체문제)는 뉴턴의 방정식으로 풀리지 않는다. 포앙카레는 태양계는 본질적으로 다체 문제이기 때문에 비선형 방정식으로 풀 수밖에 없다고 결론짓고 새로운 방정식을 구성하였다. 어떤 경우 매우 작은 변화가 행성을 큰 폭으로 움직이게 하고 충분한 시간이 지나면 궤도를 이탈할지 모른다는 결론이 나왔다. 그는 혼돈의 예측 불허성의 원인이 되는 '결정론적 계에서의 초기 조건에의 민감성'을 최초로 알았다.
12. 삼체 문제란 무엇인가?
3체문제는 오일러 시대부터 수학의 모든 영역 안에서 가장 어려운 문제 가운데 하나로 생각되어왔다. 수학적으로 이 문제는 9개의 연립미분방정식을 푸는 것으로 귀착된다. 라그랑주는 이 연립방정식을 더욱 간단한 것으로 귀착 시키는데 성공했다. 방정식의 해는 대개 물리학상의 문제가 그런 것처럼 유한의 모양이라고 기대할 수 없다. 즉 대체로 해가 존재한다면 그것은 무한급수로써 주어질 것이다. 이 급수가 변수의 일정한 구간에서 방정식을 (형식적으로) 만족하고, 또한 수렴할 때 해가 '존재한다'고 할 수 있다. 새로운 어려움은 그 수렴성을 증명하는 데 있었다. 1905년에 이르기까지 여러 가지 특수해가 발견되었다. 그러나 일반적이라고 할 수 있는 것은 어느 하나도 얻을 수가 없었다. 헬싱키의 준드만은 3체가, 세 개가 동시에 충돌하는 지극히 드문 경우를 제외하고는 해가 존재한다는 것을 증명했다. 이 해는 수치계산에 사용될 수 없었고, 실제의 천체 운동에 많은 지식을 제공하는 것도 아니었지만, 중요한 것은 그 때까지 풀 수 없었던 문제가 풀린다는 것이 증명되었다는 것이다.
달/지구/태양으로 이루어진 계의 운동을 흔히 3체문제(three body problem)라고 부른다. 그 명칭에는 충분한 이유가 있다. 뉴턴이 깔끔하게 풀었던 2체 문제와는 전혀 다르기 때문에 다른 은하나 다른 우주의 다른 행성에서 고안된 문제가 아닐까 하는 생각이 들 정도이다.
3체 문제는 거리 역제곱의 중력 법칙하에서 3개의 질량 사이에 일어나는 운동을 기술하는 방정식의 해를 요구한다. 지난 수세기 동안 많은 수학자들이 그 문제의 답을 구하기 위해 애썼다. 그러나 들로네가 계산한 근사치를 제외한다면, 수학자들은 놀랄 만큼 완벽하게 실패한 셈이다.
13. 카오스를 수학적으로 누가 정의했는가?
(1) Li-Yorke
Let I be an interval and f:I -->I be a continuous function.
Assume that f has a periodic orbit of period 3.
① f has periodic orbits of every period;
② there is an uncountable set S( subset of I) such that O(x) is aperiodic and unstable for every x(in S)
1975년 미국 메릴렌드 대학의 수학자 Yourk와 그의 제자 이천암(李天岩)이 'Period Three Implies Chaos'라는 논문을 수학 잡지에 발표했다. 그들은 이 논문에서 '카오스'라 불릴 만큼 매우 복잡한 해의 구조(임의의 자연수를 주기로 하는 무한개의 주기해와 자연수와 대응시킬 수 없을 만큼 무한히 많은 비주기해)가 존재" 하기 위한 충분 조건을 수학적으로 제시했다.
14. 한(韓)과 카오스
나비효과는 '초기값의 민감성'이다. 초기의 소수점 세자리의 변화가 나중에는 엄청난 큰 결과를 가져온다는 것이다. 사주팔자(四柱八字)야 말로 나비효과의 좋은 예가 될 수 있다. 즉, 사주팔자에서는 사람이 난 시간과 날짜가 사람의 평생운명을 좌우한다고 한다. 한의학에서는 오운육기(五運六氣)라고 하여 난 시간, 날짜, 해, 달이 그 사람의 평생 건강을 결정한다고 한다. 한의학에서는 이를 하나의 이론으로 정규과정에서 다루고 있다. 이런 동양의 지혜는 카오스 이론을 그대로 반영하고 있다. '한'의 의미 속에는 극점을 의미할 때도 있다. 공동번역 성서에선 태초를 '한처음'이라고 번역하였다. '한처음'은 더 이상 없는 원초적 초기를 의미한다. 카오스 이론에서 말하는 초기값의 민감성은 곧 한 처음 값이 전체를 차지한다는 것을 의미한다. 우리는 초기값을 종종 '첫눈에 반했다.'라고 한다. 한이란 사전적 의미 속에는 '한밤(mid-night)','한여름(mid-summer)'에서와 같이 '가운데'를 의미하는 뜻이 있다. '한가운데'로 끌어들이는 힘이 한 속에 있다. 한은 '하나'와 '여럿'을 끌어당기는 힘이 있다. 이 힘이 우주 창조의 힘이고 역사의 추진력이 되기도 한다. '한가운데'를 의미하는 이러한 한의 의미가 카오스 이론에서 중요시하는 '끌개'를 일치시켜 생각할 수 있다.
'한'의 사전적 의미 속에 '같다(同)' 는 의미가 있음을 발견하게 된다. '한데'하면 '같은 데'란 뜻이며, '한가지'하면 같은 종류의 뜻이 된다. 한의 이러한 동질성을 의미하는 것은 프랙탈이론에서 자기상사현상을 설명하기에 적합하다. 바로 한의 동일성의 의미는 프랙탈의 자기닮음이다.
'한 십분', '한 동안' 등은 정수로 표현하기 곤란할 때 사람들이 흔히 쓰는 표현이다. 이런 표현은 '어림'으로 하는 표현이다. 프랙탈 차원과 비교할 수 있다.
(출처:카오스와 문명, 동아출판사, 김상일)
15. 카오스이론의 세계관은 어떠한가?
결정론과 예측 가능성은 지금까지 자명하게 동의어로서 다루어 졌다. 이는 동일한 원인이 동일한 결과를 낳는다는 좁은 의미의 결정론만을 이해해 왔기 때문이다. 자연과학의 목적은 자연의 모든 현상을 자연법칙의 규칙으로 환원시켜 설명하는 데 있다. 여기서 유일한 전제는 완전한 인과 관계의 성립이다. 한 원인은 반드시 한 결과에 앞서야 한다. 자연의 다양성이 몇몇의 규칙으로 환원되는 것은, 즉 관찰된 결과에 대한 원인 규명이 이루어짐을 의미한다. 동일한 원인은 동일한 결과를 갖는다는 것이 지금까지 자연해석의 근간이었다.
반면에 전자기학의 아버지인 맥스웰은 이미 나름의 독특한 자연해석을 제시하였다. "동일한 원인이 동일한 결과를 낳는다는 것은 형이상학적 독단이다. 어느 누구도 그렇게 확신할 수 없다. 동일한 원인이 두 번 다시 나타나지 않으며, 결코 반복되지 않는 세계에서는 위의 생각이 적용될 수 없다." 이런 입장을 대변하는 물리적 공리는 다음과 같다. 유사한 원인이 유사한 결과를 갖는다. 이제 우리는 동일성에서 유사성으로, 절대적 엄밀성에서 다소간 폭 넓은 유사성으로 전환했다. 그는 동일한 원인이 동일한 결과는 낳는다는 좁은 의미의 결정론 대신에, 유사한 원인이 유사한 결과를 갖는다는 넓은 의미의 결정론을 이야기한다. 보통 우연과 필연은 조화될 수 없는 대립물로서 간주 되었으나 카오스 이론에서는 그렇지 않다. 카오스가 결정론적 구조를 갖는다고 말하는 것은 모순처럼 보인다. 그러나 결정론적인 것과 카오스 적인 것은 겉으로 보기에만 모순이라는 것이 카오스 이론의 기본명제이다. 이 명제에서 이야기하는 우연성은 다음의 두가지 성질로 나누어 볼 수 있다.
첫째, 현상적인 우연의 요소가 있기는 하지만 결정론적 법칙에 따르는 계에 지배되는 물리 체계가 있음을 말한다. 따라서 우연성은 숨겨진 질서 구조의 외형일 뿐이다. 즉 대상들간의 변화 운동에서 생기는 현상적 우연성이며, 인식론적으로만 인과 관계의 끈을 찾을 수 없을 뿐이다. 물리적 우연성은 처음 상태와 끝 상태의 관계가 일의적 이지는 않지만, 카오스 속에 깊숙이 놓여 있는 어떤 질서가 있다고 본다. 물리적 체계의 역학적 운동은 결정론적 법칙에 의해 지배되고 있지만, 그럼에도 불구하고 현상적 우연성을 보이는 물리체계다. 여기서 문제가 되는 것은 단순한 결정론적 방정식이 긴 시간동안 예측 불가능한 해답만을 줄 수 있다는 점이다. 체계의 상태 변화는 결정적이지만 단지 예측할 수 없을 뿐이다. 그러한 체계의 우연성은 동일한 원인이 동일한 결과를 낳는다는 좁은 의미의 인과율을 적용하지 않는다. 작은 원인이 큰 결과를 가질 수 있다. 이제 카오스 이론의 등장과 함께 좁은 의미의 인과율은 힘을 잃은 듯하다.
둘째, 대상 자체의 운동이 원래 우연적 구조를 갖고 있다는 점이다. 우연성은 기존의 선형적 수학식으로 기술이 불가능하다. 방정식의 미분값은 당연히 비선형적이다. 모든 우연적인 현상을 카오스 이론으로 설명할 수는 없다. 결정론적 카오스 현상은 모든 비선형적이지만, 비선형적 현상 모두가 결정론적 카오스 현상은 아니다. 복잡계안의 심연의 질서가 존재하는데, 이것은 부분적으로 아주 매력적인 기하학적 형식으로 환원시킬 수 있다. 무질서 체계의 우연 관계는 분명히 체계 내재적이다. 이 경우에 복잡계의 혼돈 현상은 체계의 객관적 성질인 듯 하며, 인간의 제한된 인식 능력의 부족 때문만은 아니다. 자연 세계의 숨겨진 기하학적인 아름다움과 살아 있는 유기체의 구조를 기계론적으로 설명할 수 없지만, 내재적 질서가 있음은 어느 누구도 부정하지 않는다.
(출처: 부분의 합은 전체인가, 소나무)
16. 카오스는 무질서를 의미하는가?
카오스는 두가지를 의미한다. 하나는 분자들의 움직임처럼 확률적으로 밖에 표현할 수 없는 경우를 비결정론적 카오스라 한다. 요즘은 결정론적인 카오스를 간단히 카오스라 흔히 부른다.
랜덤은 전혀 질서가 없는 상태이다. 카오스의 결정론은 랜덤 일보 직전의 무질서를 의미한다. 시간의 경과에 따라 살펴보자.
(1) 처음에는 질서정연했다.
(2) 질서가 무너지기 시작한다.
(3) 카오스
(4) 무작위(random)
17. 결정론과 비결정론은 어떻게 다른가?
선형법칙은 두 가지 성질을 가진다. v=0.4 t +9를 생각해 보자.
(1) 초기값을 하나 정하면 t 에서의 값은 단지 하나가 결정된다.
(2) 초기값을 조금 변형시키면 0.4를 0.42 로 조금 변화시키면 v는 조금밖에 변하지 않는다.
y=2n 을 생각해 보자. 선형은 아니지만 초기값에 대해 하나의 y가 결정된다.
비결정론이란 동전던기기와 주사위 던지기가 있다.
18. 역학계(dynamical system)란 무엇인가?
수열 xn 이 식 xn+1=f(xn)으로 표현할 수 있는 경우를 역학계라 한다. 초기값 x0 에서 출발하여 x1, x2, ... 로 차례차례 결정되어 가는 수열을 역학계의 초기값 x0인 경우의 궤도(orbit) 이라 한다.
19. 카오스의 성질
수학자들은 f(x)=ax(1-x)와 같은 변환의 반복으로 나타나는 카오스의 세가지 공통 특성에 대하여 일반적으로 동의한다. 세가지 특성은 혼합성, 주기성, 초기 조건에의 민감성이다.
(1) 혼합성 : 길이가 0이 아닌 두 구간 I 와 J에 대하여, 반복을 통하여 구간 J에 오게되는 점들이 항상 구간 I 내에 존재한다. 반복에서 반복값들이 순환적인 패턴으로 나타나는 점들은 주기적이다.
(2) 주기성 : 주기점들은 [0, 1]의 어떤 작은 구간에서든지 주기점 가까이에 많은 점들이 있다.
(3) 초기점의 위치를 조금만 변화시켜도 반복된 수열에서는 다른 결과를 나타낸다. 이는 초기 조건에 대한 민감성이 강하다는 것을 보여준다.
20. 파이겐바움 분기도
① x0=0.1 a=2.9 (나선형 끌개, 2주기)
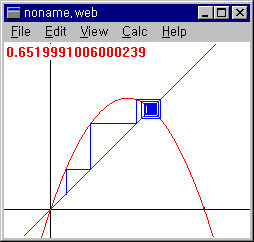
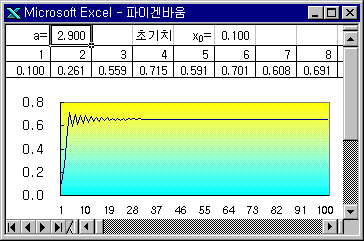
② x0=0.1 a=3.84 (3주기)
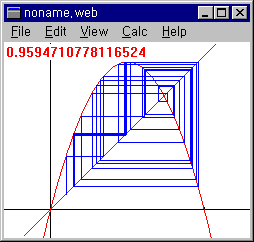
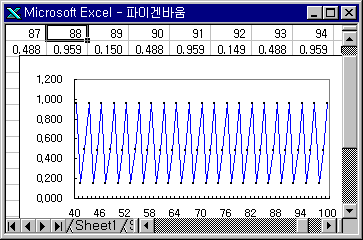
③ x0=0.1 a=3.50 (4주기)
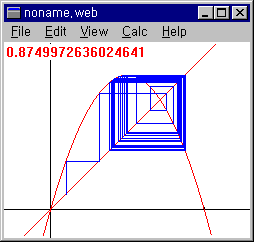
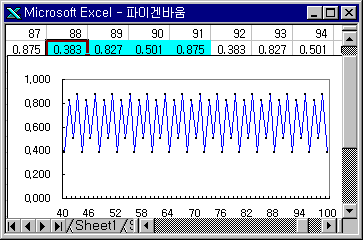
④ x0=0.1 a=3.74 (5주기)
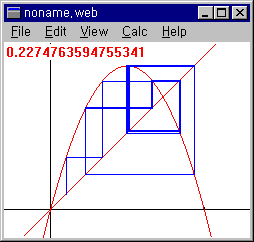
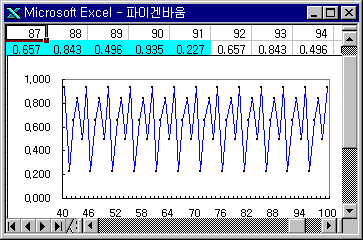
④ x0=0.1 a=3.90(카오스)
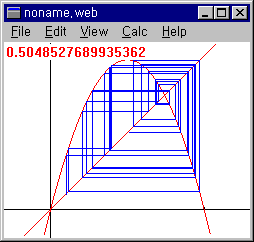
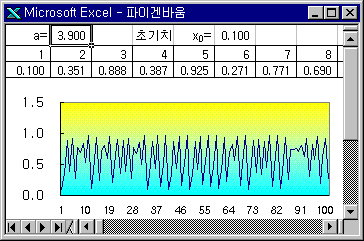
⑤ 분기와 프랙탈
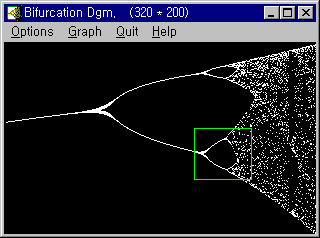
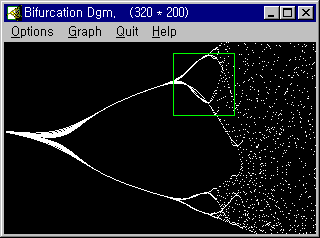
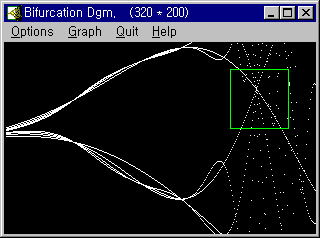
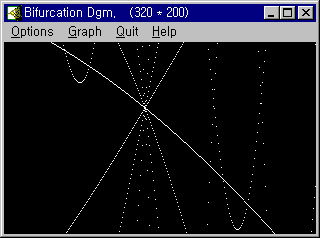
21. 카오스 이해를 위한 몇가지 정의
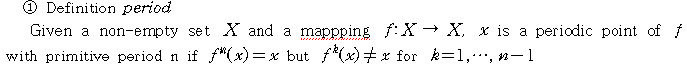

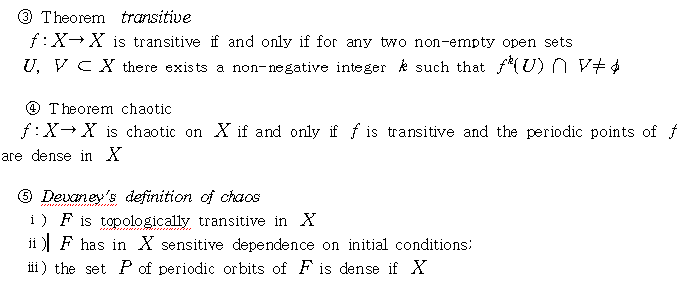
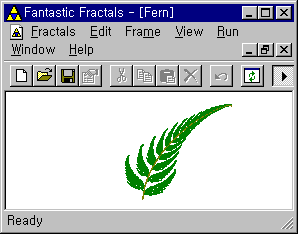
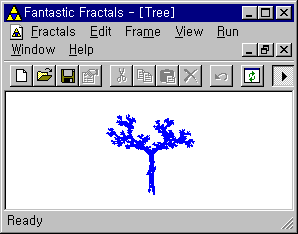
22. L-system 이란?
린덴마이어는 수학적 공식을 사용해서 식물의 성장과정을 기술하는 문제에 대해 생각하기 시작했다. 그가 사용한 도구는 형식 언어학 이론이었다. 린덴마이어 계는 부분적으로 세포 자동자와 공통점을 갖고 있었다. 즉, 불연속인 시간 단계에 따라 진행되며, 매시간 단계마다 각각의 상징은 가장 먼저 그 이웃을 살펴보고, 그런 다음 어떤 상징이 다음 시간 단계에 나타날 것인가를 알아보기 위해 특수한 규칙을 참조하게 된다.
하나의 알고리즘이 식물의 성장처럼 극히 복잡해 보이는 결과를 예측할 수 있으리라는 가정은 무척 놀랍게 들린다. 이것이 가능하다면 복잡한 자연의 자기 조직 원리가l 순수한 수학과 컴퓨터 과학의 영역에서 구현될 수 있음을 입증하게 될 것이다.
규칙 1 : 현재 단계에서 a는 다음 단계에서 ab로 된다.
규칙 2 : 현재 단계에서 b는 다음 단계에서 a가 된다.
이 규칙들은 'L-계'라는 이름으로 불리게 되었다. 린덴마이어는 식물의 성장 시스템을 기술하는 순수한 수학적 구성물로 L-계를 사용하려 했다. L-계를 사용함으로써 자연 속에서 실제로 일어나는 일과 관련을 갖든 갖지 않든 간에 무한한 집합의 성장 규칙들을 만들어 낼 수 있었다.
1970년 네델란드 유트레히트 대학의 두 대학원생인 벤 헤스퍼와 파우리네 호게베크는 L-계가 실제로 식물 형태를 그려 낼 수 있을 지에 대해 의문을 품었다. 그 실험 결과는 식물 자체나 식물의 모델이 아니라 자연과 논리를 부모로 둔, 자식 즉 둘 사이의 잡종일 것이다. 이 들은 1974년 3,584개에 달하는 나무 집합을 연구하였다.





















Facebook 댓글